Basic Stats
Traditional statistics definitely has it’s place in a modern data scientists toolkit. Not only as the precursor to machine learning but also as a powerful tool in-and-of itself.
Before going too far, we have to address the fight between Bayesian and Frequentist statisticians. If you aren’t familiar, these two camps have been engaged in a bitter debate that frankly doesn’t really serve anyone. Both approaches have a large amount of value in the correct context. We’ll talk about both.
Treatment effectiveness

Sample distributions
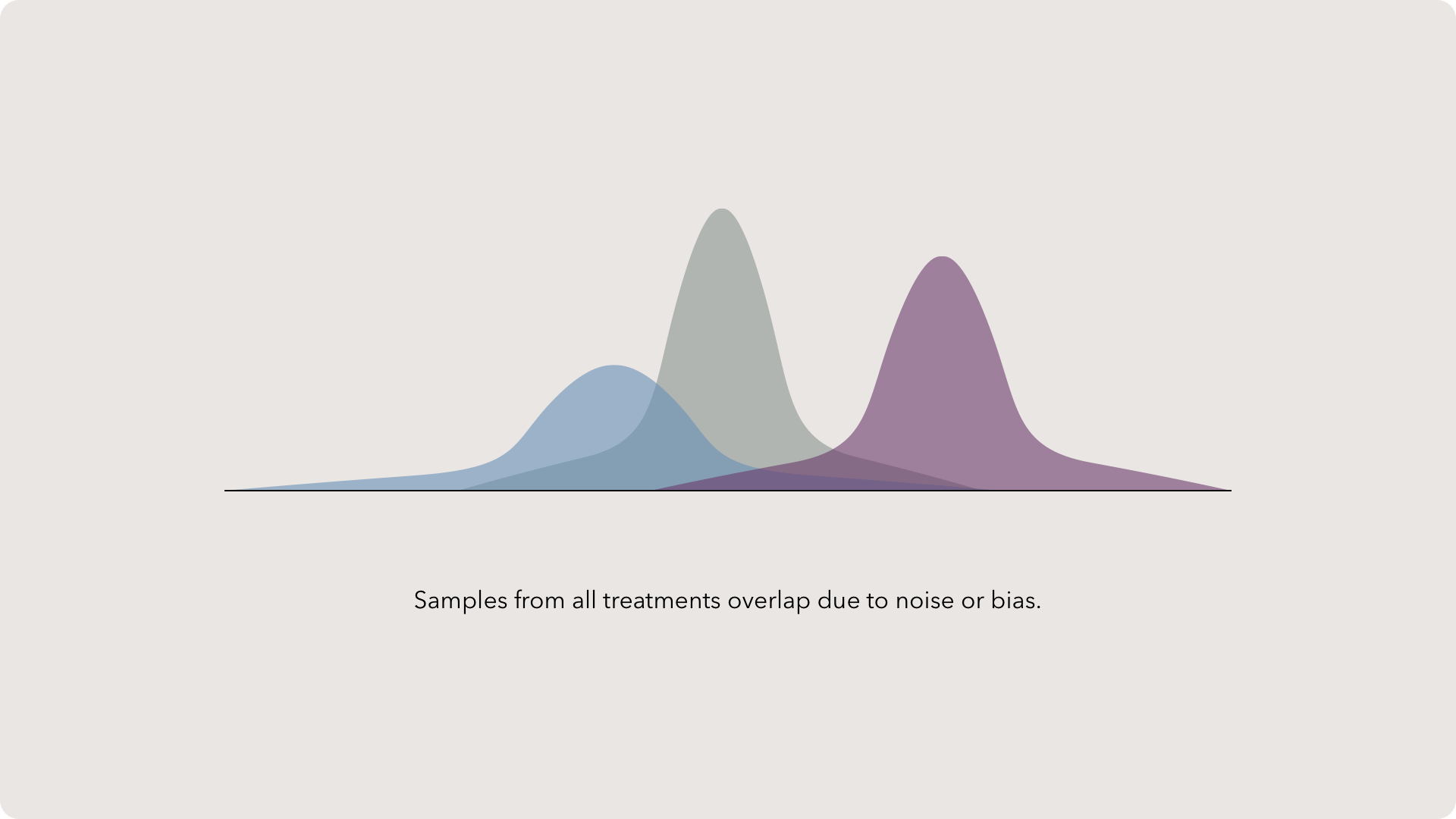
Distributions are the represented by a value on the x-axis with the frequency on the y-axis. The more a value occurs in the data set, the higher the peak around that point in a distribution.
Distribution attributes
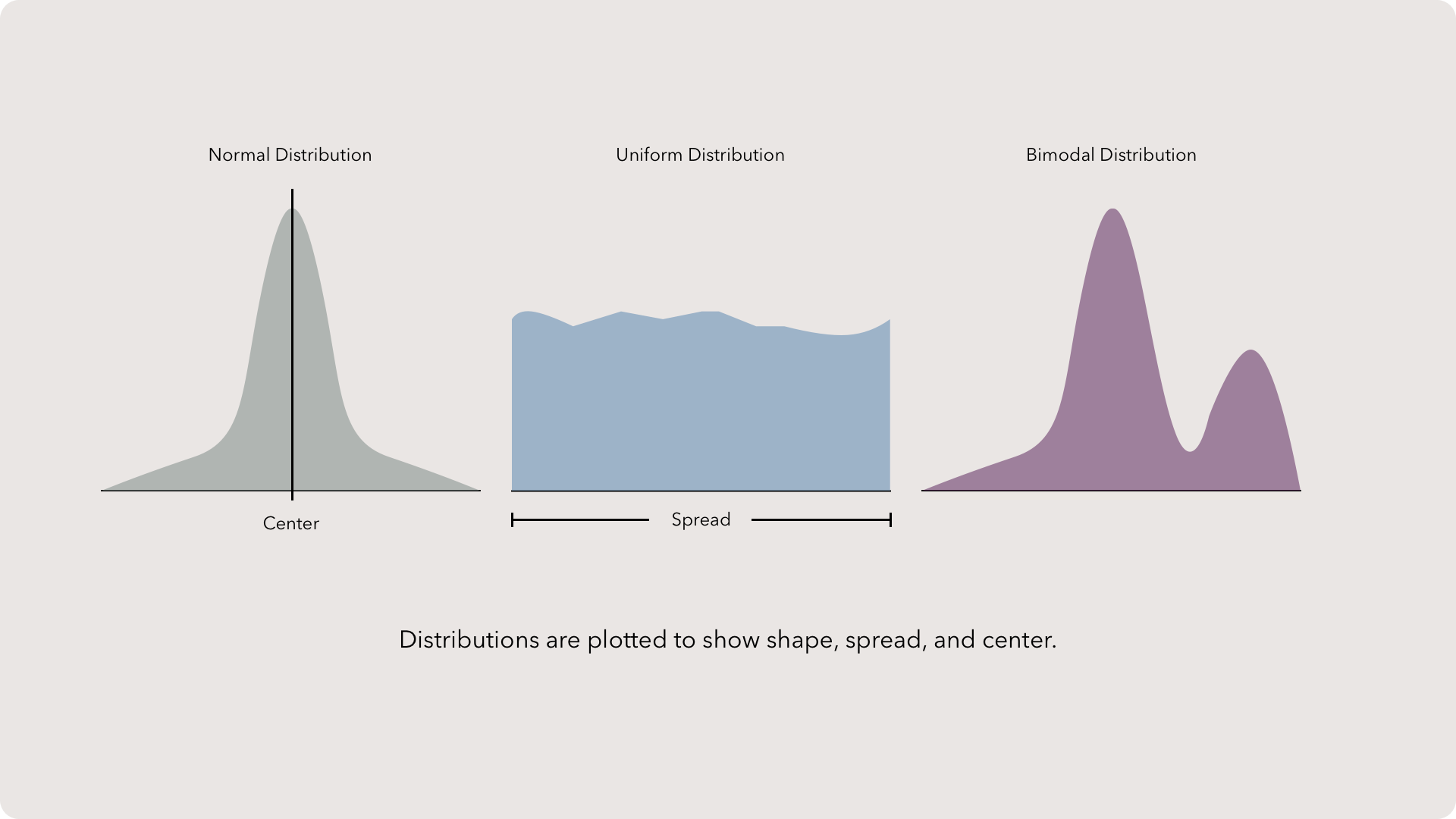
We describe distributions with three key attributes: the center, the spread and the shape.
The center is your typical measure of central tendency. This is either the mean, median or mode. As we’ll see in a second, median is a robust measure but most folks use mean simply since its more commonplace. In case your brain is foggy, the median is the middle value of when you line up all the data in order.
Spread represent the range of values. Think about the distance between the minimum value to the maximum and that is how far the data spreads out.
Finally, shape. Your data will in all sorts of shapes when you plot the distribution. However, it is extremely common for the data to form a normal distribution, or bell curve. This distribution has a large bulge in the center than descends rapidly and spreads out in tails. The law of large numbers describes the natural phenomenon where the more data is collected from a population, the closer the sample space will look like a normal distribution.
You might also encounter uniform and bimodal distributions as well. Uniform distributions occur when the data has roughly the same frequency. Think of a plateau, where every value is equally likely to occur. Bimodal distributions are like normal distributions, but have two peaks. Yes, you might have multi-modal distributions but that likely indicates your are not creating proper treatment groups.
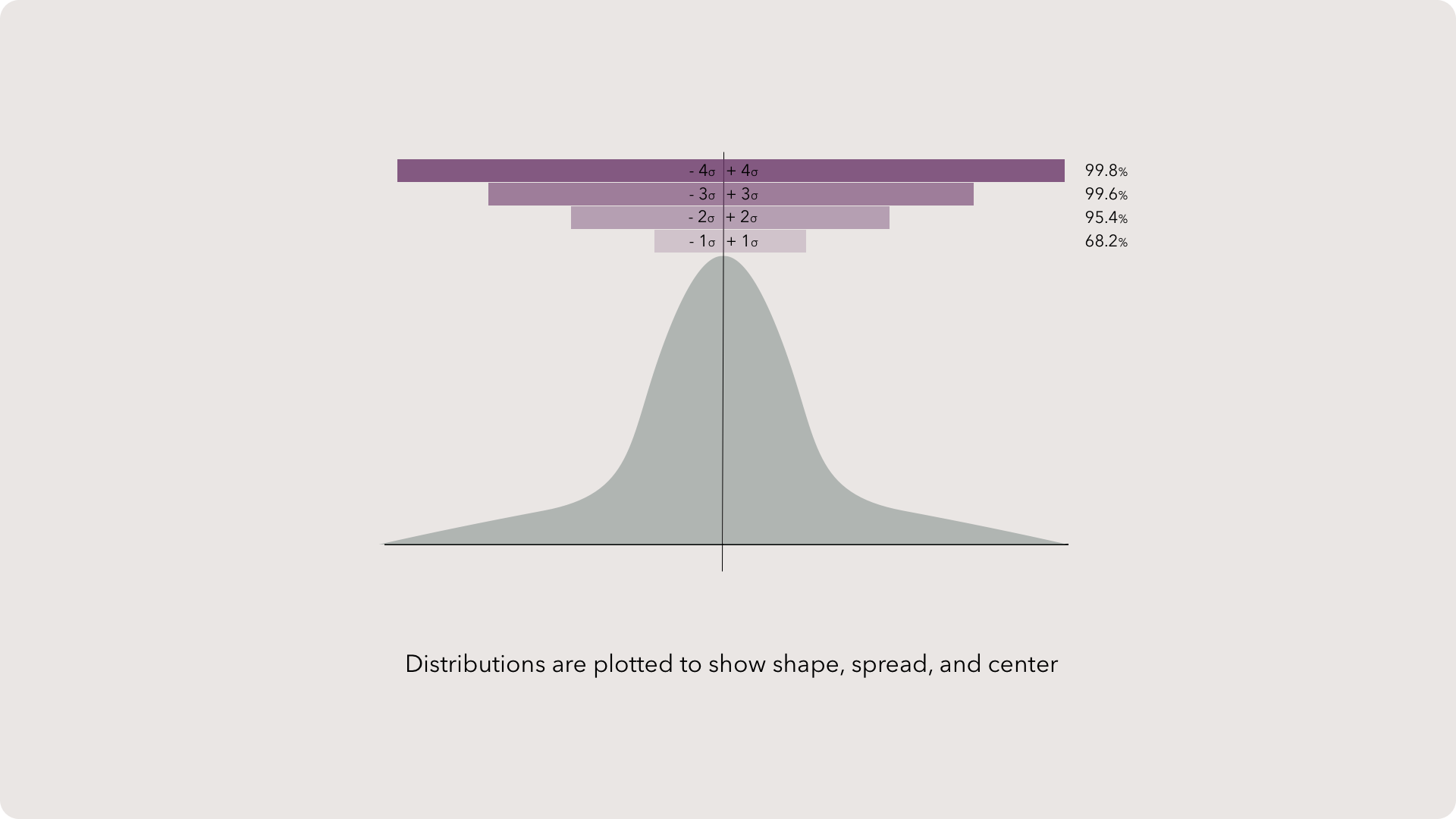
Standard Deviations
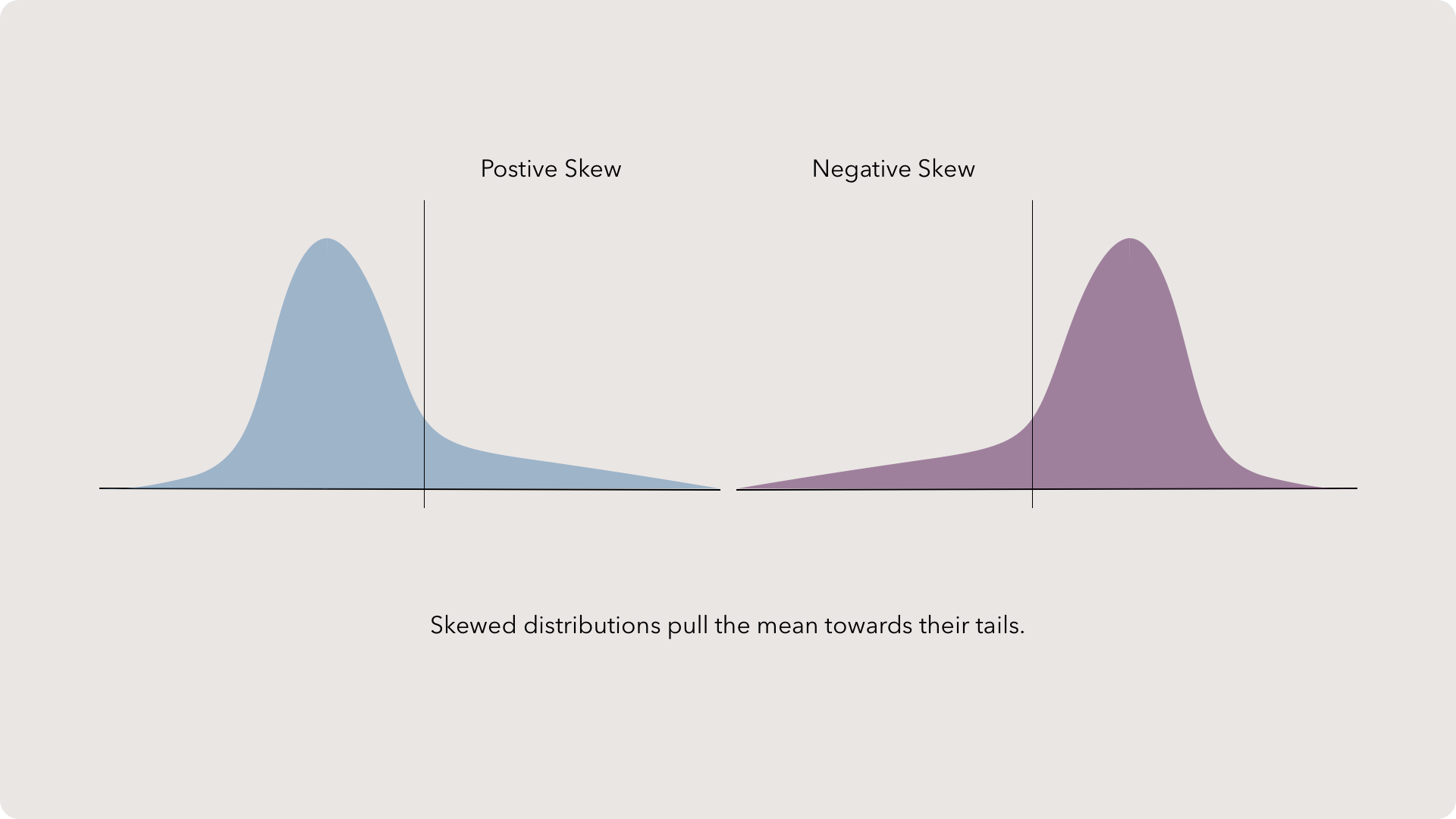
Skew
Hypothesis testing

Hypothesis testing is broken down into four key parts. First, we need to declare a hypothesis and its alternative — more on this soon. Then we use our data to calculate a p-value. The calculation doesn’t really matter for this short course as your software will have this built-in. We compare our p-value to the alpha (again, more soon), and decide if we can reject our null hypothesis.
Let’s slow down that interpretation. In statistics, we can’t “prove” anything. Chance and bias always play a role in how our data can be interpreted. Instead, we can make statements about the likelihood of our statement being supported by our observations opposed to just seeing our results by chance. Imagine you win the lottery, it would be inaccurate to state that winning is easy or common. You just got very lucky. The rejection of a hypothesis uses safeguards so a researcher must state how likely the results of a treatment would be similar result would be due to luck alone.
Finally, we communicate our findings back in a way that any audience could understand. Don’t skip this step. Please don’t. Your job is to help people learn new things about the universe, not hoard knowledge behind archaic formulations.
Declaring a hypothesis

We use the phrase “fail to reject”. Because we cannot absolutely prove a hypothesis, we must either support or not support it based on whether we can negate it. If we reject the null hypothesis then logically we must support the alternative hypothesis. If the null hypothesis cannot be rejected then there is not enough evidence to support the alternative hypothesis.
P-Values
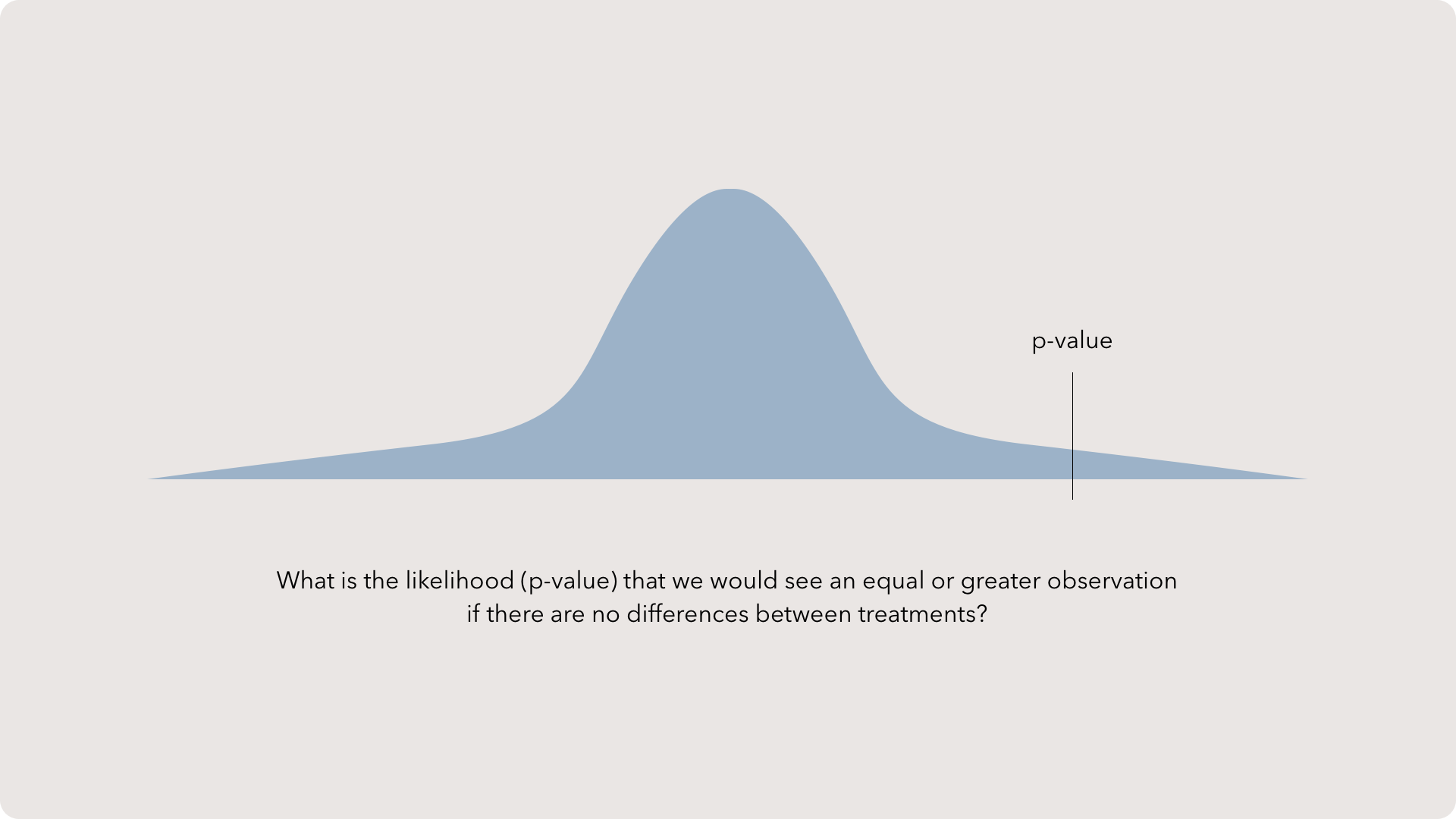
Note: This alpha value is entirely arbitrary and a valid criticism of Frequentist statistics. Some scholarly journals are even disallowing statistical interpretation based on significance.
Confidence Intervals
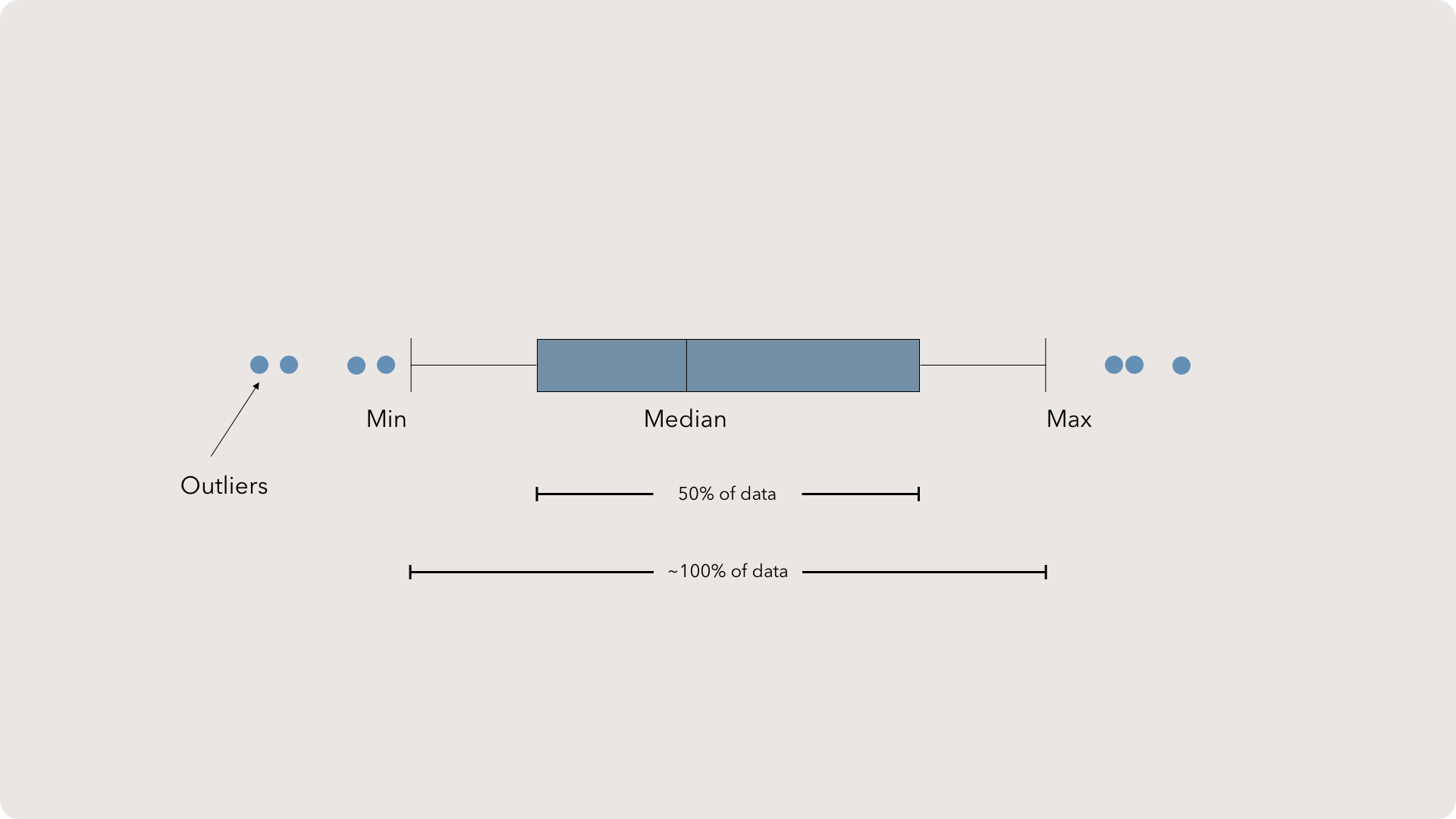
Commonly, scientists use a 95% confidence interval range or plus-and-minus two standard deviations. This protects the CI from most outliers while providing the maximum amount of range for analysis.
CI as Intervals
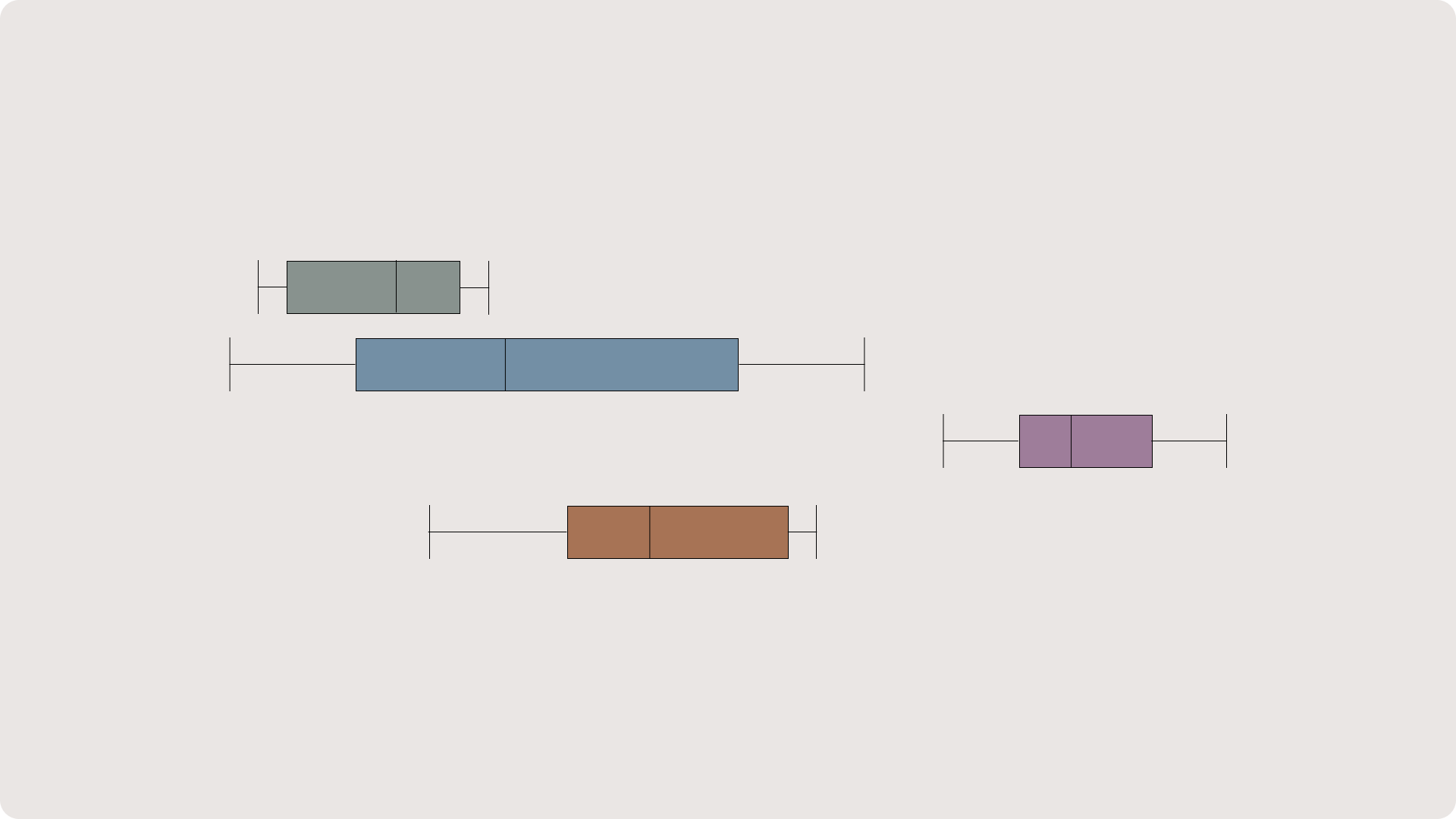
Confidence Intervals can be used to replace hypothesis testing with p-values. This has the advantage of being simpler to understand. If the confidence intervals don’t overlap at all then you have evidence suggesting that the two groups behaved differently. Likewise, if the intervals overlap over the center, then there is evidence supporting no difference between groups.